Many people like maths because it is straightforward – you’re either right or wrong…  but that’s not the whole story.  Looking at a student’s workings is essential to identify where their misunderstanding is, but not everyone writes down what they were doing.  This requires them to keep information in short-term memory which has a limited capacity, leaving less processing power for the calculations.  PLUS, part of the point is to be able to communicate and perhaps use part of a calculation further on in the question.  When it comes to exams the workings are the marks.  So not showing workings is a #bigmistake!  Not writing them down when you’re learning will hamper you and lose you marks when it really matters.

If I were to have a ‘special power’, it would be to be able to read minds.  As a teacher, I need to identify what concept is unclear or part of the procedure is confused.  Without the ability to mindread I rely on workings.  Errors should be picked up and corrected as soon as physically possible.  Otherwise, the student will continue to make the error thinking they are doing the right thing and thereby learn the method complete with the mistake.

Things to look out for in basic computation include:

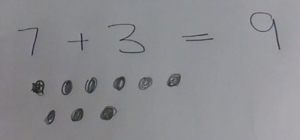Number bonds not yet sound, this could indicate that further investigation and intervention is required.  In the example here, dots have been drawn to represent the numbers but there are 6 rather than 7 dots on the top line so when they’ve been counted the answer is wrong.  There are 5 number facts that make up number bonds but children need to have a real sense of them to appreciate and use them, not just learn them by rote.  Using marks / dots or fingers is fine but even if the correct number of dots had been drawn it is important that the child is corrected if they try to count too quickly, miss our double count.  So early stages need supporting.

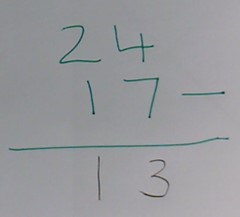Misunderstanding with subtraction can be linked to the original language used as demonstrated here the 4 in the units’ column has been subtracted from the 7 rather than borrowing from the tens column.  Taking the smaller number from the larger one relates to the whole number not each column of it.

As soon as such errors are seen they should be addressed otherwise the error becomes imbedded and then has to be unlearnt.